Chapter 2
Learn smarter, practice harder. Skill-building made simple, fun, and effective. Mprezz turns effort into expertise
Polynomials
Exercise 2.1
Question 1 (i)
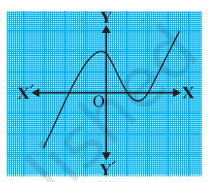
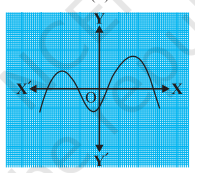
The graphs of y = p(x) are given in figure below, for some polynomials p(x). Find the number of zeroes of p(x), in each case.
Solution:
Looking at the provided graph, the graph intersects the x-axis at 3 distinct points.
Answer: This means the polynomial p(x) has no real zeroes.
____________________________________________________________________________
Question 1 (ii)
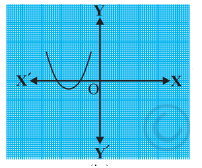
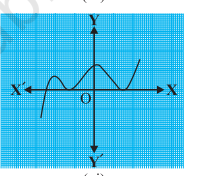
The graphs of y = p(x) are given in Figure below, for some polynomials p(x). Find the number of zeroes of p(x), in each case.
Solution:
The graph intersects the x-axis at only one point. This means the value of the polynomial becomes zero at one point only.
Answer: 1 zero
____________________________________________________________________________
Question 1 (iii)
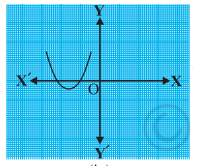
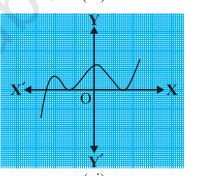
The graphs of y = p(x) are given in Figure below, for some polynomials p(x). Find the number of zeroes of p(x), in each case.
Solution:
The graph crosses the X-axis three times.
Therefore, the number of zeroes of p(x) is 3.
____________________________________________________________________________
Question 1 (iv)
The graphs of y = p(x) are given in Figure below, for some polynomials p(x). Find the number of zeroes of p(x), in each case.
Solution:
The graph is tangent to the X-axis at one point.
That point is a double root (a repeated root).
Even though the curve touches the X-axis only once, algebraically it counts as two zeroes because it's a root of multiplicity 2.
Answer: The number of zeroes of p(x) is 2.
____________________________________________________________________________
Question 1 (v)
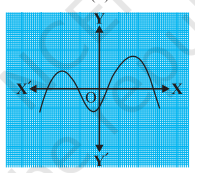
The graphs of y = p(x) are given in Figure below, for some polynomials p(x). Find the number of zeroes of p(x), in each case.
Solution:
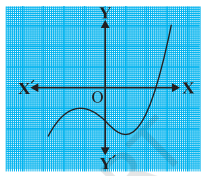
The graph crosses the X-axis four times.
Each intersection with the X-axis represents a real zero (root) of the polynomial.
Therefore, the number of zeroes of p(x) is 4.
____________________________________________________________________________
Question 1 (vi)
The graphs of y = p(x) are given in Figure below, for some polynomials p(x). Find the number of zeroes of p(x), in each case.
Solution:
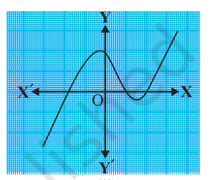
The graph intersects the X-axis at three distinct points.
Each intersection represents a real root (zero) of the polynomial.
Therefore, the number of zeroes of p(x) is 3.
____________________________________________________________________________
Exercise 2.2
Q1. Find the zeroes of the following quadratic polynomials and verify the relationship between the zeroes and the coefficients.
(i)
Solution:
Step 1: Find the zeroes
We are given the polynomial: x² − 2x − 8
We will factor it.
We look for two numbers that:
Multiply to give -8 (the constant term)
Add to give -2 (the middle term)
The numbers are -4 and +2
So we can write: x² − 2x − 8 = (x + 2)(x − 4)
Now, set each factor equal to zero:
x + 2 = 0 → x = -2
x − 4 = 0 → x = 4
Answer: So the zeroes are -2 and 4
____________________________________________________________________________________
(ii) 4s² – 4s + 1
Solution:
Step 1: Find the zeroes
Use the quadratic formula: s = (-b ± √(b² – 4ac)) / 2a
Here, a = 4, b = -4, c = 1
s = (4 ± √(16 – 16)) / 8
s = (4 ± 0) / 8
s = 4 / 8
s = 1/2
Answer: So, the zeroes are s = 1/2 and s = 1/2
____________________________________________________________________________________
(iii) 6x² – 7x – 3
Solution:
Step 1: Find the zeroes
We’ll use the quadratic formula:
x = (-b ± √(b² – 4ac)) / 2a
Here:
a = 6, b = -7, c = -3
x = (7 ± √((-7)² – 4 × 6 × (-3))) / (2 × 6)
x = (7 ± √(49 + 72)) / 12
x = (7 ± √121) / 12
x = (7 ± 11) / 12
So,
x = (7 + 11) / 12 = 18 / 12 = 3/2
x = (7 – 11) / 12 = -4 / 12 = -1/3
Answer: Zeroes are x = 3/2 and x = -1/3
____________________________________________________________________________________
(iv) 4u² + 8u
Solution:
Step 1: Find the zeroes
Factor the expression:
4u² + 8u = 4u(u + 2)
Now set each factor equal to zero:
1. 4u = 0 → u = 0
2. u + 2 = 0 → u = -2
Answer: Zeroes are u = 0 and u = -2
____________________________________________________________________________________
(v) t² – 15
Solution:
Step 1: Find the zeroes
This is a difference of squares:
t² – 15 = 0
⇒ t² = 15
⇒ t = √15 or t = –√15
Answer: Zeroes are t = √15 and t = –√15
____________________________________________________________________________________
(vi) 3x² – x – 4
Solution:
Step 1: Find the zeroes
We use the quadratic formula:
x = (–b ± √(b² – 4ac)) / 2a
Here, a = 3, b = –1, c = –4
x = (1 ± √(1² – 4 × 3 × (–4))) / (2 × 3)
x = (1 ± √(1 + 48)) / 6
x = (1 ± √49) / 6
x = (1 ± 7) / 6
Now calculate both values:
x = (1 + 7) / 6
= 8 / 6
= 4 / 3
x = (1 – 7) / 6
= –6 / 6
= –1
Answer: Zeroes are: x = 4/3 and x = –1
____________________________________________________________________________________
Exercise. 2.2
Question 2: Find a quadratic polynomial each with the given numbers as the sum and product of its zeroes respectively.
Solution:
Let the zeroes of the quadratic polynomial be α and β.
We are given:
Sum of zeroes = 1/4
Product of zeroes = −1
We use the general form of a quadratic polynomial based on its zeroes:
x² − (sum of zeroes)x + product of zeroes
Now substitute the given values:
x² − (1/4)x − 1
This is a quadratic polynomial with fractional coefficient. To remove the fraction, multiply the entire expression by 4 (the denominator of 1/4):
4 × [x² − (1/4)x − 1] = 4x² − x − 4
Answer: The required quadratic polynomial is: 4x² − x − 4
____________________________________________________________________________________
Q2
Solution:
Let the zeroes of the quadratic polynomial be two numbers whose:
Sum = √2
Product = 1/3
We use the standard form:
x² − (sum of zeroes)x + product of zeroes
Substitute the given values:
x² − (√2)x + 1/3
To eliminate the fraction, multiply the entire expression by 3:
3 × [x² − √2x + 1/3] = 3x² − 3√2x + 1
Answer: The required quadratic polynomial is: 3x² − 3√2x + 1
____________________________________________________________________________________
Q2
Solution:
Let the two zeroes be: 0 and √5
We use the form: (x − zero1) (x − zero2)
Substitute the values:
(x − 0)(x − √5) = x(x − √5)
Now multiply:
x × (x − √5) = x² − x√5
Answer: The required quadratic polynomial is : x² − x√5
____________________________________________________________________________________
Q2
Solution:
Sum of zeroes = 1
Product of zeroes = 1
The general form of a quadratic polynomial is:
x² – (sum of zeroes) x + product of zeroes
Substitute the values:
x² – 1x + 1
Final Answer: x² – x + 1
____________________________________________________________________________________
Q2:
Solution:
Sum of zeroes = –1/4
Product of zeroes = 1/4
Using the standard form:
x² – (sum of zeroes)x + product of zeroes
Substitute the values:
x² – (–1/4)x + 1/4
x² + (1/4)x + 1/4
To remove fractions, multiply all terms by 4:
4x² + x + 1
Final Answer: 4x² + x + 1
____________________________________________________________________________________
Q2:
Solution:
x² - (sum of zeroes)x + product of zeroes
Here,
Sum of zeroes = 4
Product of zeroes = 1
Substitute these values into the formula: x² - 4x + 1
Answer: The required quadratic polynomial is: x² - 4x + 1

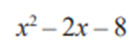
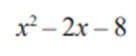
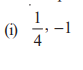
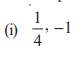
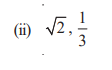
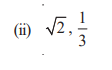
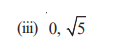
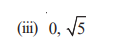
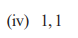
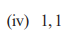
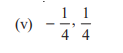
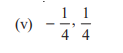
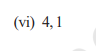
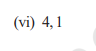
© 2024. All rights reserved.
Professor of Practice
Bridging academia and industry through innovative teaching and real-world experience for academic success.
